Gruppo circolare

In matematica, il gruppo circolare (indicato in grassetto da lavagna con ${\displaystyle \mathbb {T} }$ o in semplice grassetto con T) è il gruppo moltiplicativo di tutti i numeri complessi con valore assoluto pari a 1, cioè il cerchio unitario nel piano complesso,

${\displaystyle \mathbb {T} =\{z\in \mathbb {C} :|z|=1\},}$

dotato dell'ordinaria moltiplicazione del campo complesso.

Il gruppo circolare forma un sottogruppo di C^×, il gruppo moltiplicativo di tutti i numeri complessi non nulli. Poiché C^× è abeliano, segue che anche T lo è. La notazione T per il gruppo circolare deriva dal fatto che Tⁿ (il prodotto diretto di T con sé stesso n volte) è geometricamente un n-toro. Il gruppo circolare è quindi un 1-toro.

Introduzione elementare

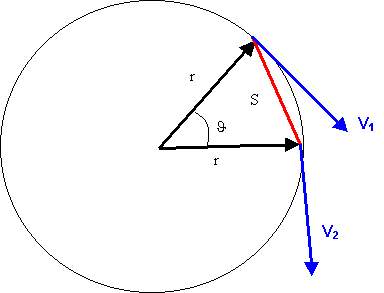
Un modo per pensare al gruppo circolare è che esso descrive come sommare gli angoli, quando sono permessi solo angoli tra 0° e 360°. Per esempio, il diagramma mostra come aggiungere 150° a 270°. La risposta dovrebbe essere 150° 270° = 420°, ma quando si pensa in termini del cerchio unitario, bisogna "dimenticare" il fatto che si è fatto un giro attorno al cerchio. Quindi correggendo la risposta di 360° ci dà 420° − 360° = 60°.

Un'altra descrizione è in termini della ordinaria addizione, usando solo numeri tra 0 e 1. Per fare questo, si devono dimenticare le cifre prima della virgola decimale. Per esempio, calcolando 0.784 0.925 0.446 la risposta potrebbe essere 2.155, ma tirando via il 2, la risposta (nel cerchio unitario) è 0.155.

Struttura topologica e analitica

Il gruppo circolare non è solo un gruppo algebrico astratto. Esso ha una topologia naturale quando è considerato come sottospazio del piano complesso. Poiché la moltiplicazione e l'inversione sono funzioni continue su C^×, il gruppo circolare ha la struttura di un gruppo topologico. Inoltre, poiché il cerchio unitario è un sottoinsieme chiuso e limitato del piano complesso, il gruppo unitario è un sottogruppo chiuso di C^× (visto come gruppo topologico). Dal punto di vista topologico, il gruppo circolare è compatto.

Si può dire di più. Il cerchio è una varietà topologica 1-dimensionale reale e la moltiplicazione e l'inversione sono mappe reali e analitiche sul cerchio. Questo dà al gruppo circolare la struttura di un gruppo di Lie 1-dimensionale. In effetti, a meno di un isomorfismo, è l'unico gruppo di Lie connesso, compatto1-dimensionale. Inoltre, ogni gruppo di Lie n-dimensionale, compatto e connesso è isomorfo a Tⁿ.

Isomorfismi

Il gruppo circolare prende varie forme in matematica. Sono elencate alcune delle più comuni. In particolare, si può mostrare che

${\displaystyle \mathbb {T} \cong {\mbox{U}}(1)\cong {\mbox{SO}}(2)\cong \mathbb {R} /\mathbb {Z} .}$

L'insieme di tutte le 1×1 matrici unitarie coincide chiaramente con il gruppo circolare; la condizione di unitarietà è equivalente alla condizione che gli elementi abbiano valore assoluto 1. Quindi, il gruppo circolare è canonicamente isomorfo a U(1), il primo gruppo unitario.

Il gruppo circolare è quindi isomorfo al gruppo ortogonale speciale SO(2). Questo ha l'interpretazione geometrica che la moltiplicazione per un numero complesso unitario è una rotazione proprio del piano complesso, e ogni tale rotazione è di questa forma.

Rappresentazioni

Le rappresentazioni del gruppo circolare sono semplici da descrivere. Segue dal lemma di Schur che le rappresentazioni complesse irriducibili di un gruppo abeliano sono 1-dimensionali. Poiché il gruppo circolare è compatto, ogni rappresentazione ρ: T → GL(1, C) ≅ C^×, deve prendere valori in U(1)≅ T. Quindi, le rappresentazioni irriducibili del gruppo circolare sono gli omomorfismi tra il gruppo circolare e se stesso. Ogni tale isomorfismo è nella forma

${\displaystyle \phi _{n}(e^{i\theta })=e^{in\theta },\qquad n\in \mathbb {Z} .}$

Queste rappresentazioni sono tutte inequivalenti. La rappresentazione φ_-n è la coniugata di φ_n,

${\displaystyle \phi _{-n}={\overline {\phi _{n}}}.}$

Queste rappresentazioni sono i caratteri del gruppo circolare. Il gruppo dei caratteri di T è chiaramente un gruppo ciclico infinito generato da φ₁:

${\displaystyle \mathrm {Hom} (\mathbb {T} ,\mathbb {T} )\cong \mathbb {Z} .}$

Le rappresentazioni irriducibili reali del gruppo circolare sono le rappresentazioni 1-dimensionali e le rappresentazioni

${\displaystyle \rho _{n}(e^{i\theta })={\begin{bmatrix}\cos n\theta &-\sin n\theta \\\sin n\theta &\cos n\theta \\\end{bmatrix}},\quad n\in \mathbb {Z} ^{ }.}$

che prendono valori in SO(2). Qui si hanno solo n interi positivi poiché la rappresentazione ${\displaystyle \rho _{-n}}$ è equivalente a ${\displaystyle \rho _{n}}$.

Voci correlate

• Rotazione nel piano complesso
• Circonferenza unitaria
• Gruppo unitario
• Gruppo ortogonale
• Gruppo di Lorentz